|
|
每周考点
华工考研每周考点:主要是华工各专业考研核心考点,帮助大家快速把握考试关键,进行快速查缺补漏。
相关科目:804高分子物理
相关知识点:聚合物的力学性能(2)
#1、聚合物的力学性能(2)
3. 粘弹性
3.1 基本概念
理想弹性:一个理想的弹性体,当受到外力后,平衡形变是瞬时达到的,与时间无关。形变除去后,形变立刻回复。
理想粘性:一个理想的粘性体,受到外力后,形变是随时间线性发展的。外力除去后,形变不能回复。
粘弹性:高分子材料的形变性质是与时间有关的,这种关系介于理想弹性体和理想粘性体之间,因此高分子材料常被称为粘弹性材料。
力学松弛:高聚物的力学性质随时间的变化统称为力学松弛,最基本的有:蠕变、应力松弛、滞后和力学损耗。
3.2 基本的力学松弛现象
蠕变:定义在一定的温度和较小的恒定外力作用下,材料的形变随时间的增加而逐渐增大的现象。
聚合物蠕变过程中的形变机理分析从分子运动和变化的角度看,蠕变过程包括下面三种形变:普弹形变、高弹形变、粘性流动。
普弹形变:当高分子材料受到外力作用时,分子链内部的键长和键角立刻发生变化,这种形变量是很小的,称为普弹形变,外力除去后,普弹形变可以立刻回复。
高弹形变:分子链通过链段运动逐渐伸展的过程,形变量比普弹性变大得多,形变与时间成指数关系。外力除去后,高弹形变是逐渐回复的。
粘性流动:分子间没有化学交联的线形高分子,还会产生分子间的相对滑移,称为粘性流动,外力除去后,粘性流动是不能回复的。
普弹形变和高弹形变称为可逆形变,而粘性流动称为不可逆形变。由于粘性流动是不能回复的,因此对线性高聚物来说,当外力除去后总会留下一部分不能回复的形变,称为永久形变。
影响蠕变的外界因素蠕变与温度、外力有关,温度过低,外力太小,蠕变很小且很慢,不易觉察;温度过高、外力过大,形变发展过快,也感觉不出蠕变现象;在恰当的外力下,通常在Tg以上不远,链段可以运动,但运动时受到的内摩擦力较大,只能缓慢运动,则可观察到明显的蠕变现象。
蠕变与分子结构之间的关系:聚合物链的刚性越大,抗蠕变性能越好;交联可以减小分子间滑移而造成的不可逆形变。
应力松弛:概念温度和形变保持不变,高聚物内部的应力随时间增加而逐渐衰减。
机理:应力松弛和蠕变是一个问题的两个方面,都反映高聚物内部分子的三种运动情况。当高聚物一开始被拉长时,其中分子处于不平衡的构象,要逐渐过渡到平衡构象,也就是链段顺着外力的方向运动以减少或消除内部应力。
影响因素:
温度:如果温度很高,远超过Tg,链段运动时受到的内摩擦力很小,应力松弛很快,甚至几乎觉察不到。如果温度太低,比 Tg 低得多,虽然链段受到很大的应力,但由于内摩擦力很大,链段运动的能力很弱,应力松弛极慢,也不容易觉察得到。只有在玻璃化温度附近几十度范围内,应力松弛现象比较明显。
结构:对于交联高聚物,由于分子间不能滑移,所以应力不会松弛到零,只能松弛到某一数值,因此,橡胶制品都是经过交联的。
滞后现象:高聚物在交变应力作用下,形变落后于应力变化的现象就称为滞后现象。
机理:滞后现象的发生是由于链段运动要受到内摩擦力的作用,当外力变化时,链段运动还跟不上外力的变化,所以形变落后于应力,有一个相位差。
影响滞后的因素:
柔性:高聚物的滞后现象与其本身的化学结构有关,一般刚性分子的滞后现象小,柔性分子的滞后现象严重。
频率:如果外力作用的频率低,链段来得及运动,滞后现象很小;外力作用频率很高,链段根本来不及运动,聚合物好象一块硬的材料,滞后现象也小;只有外力作用的频率不太高时,链段可以运动,但又跟不上,才出现较明显的滞后现象。
温度:温度很高时,链段运动很快,形变几乎不滞后于应力的变化;温度很低时,链段运动 速度很慢,形变来不及发展,因而也无所谓滞后;只有在Tg上下几十度的范围,链段充分运动,但又跟不上,滞后现象严重 。因此增加外力频率和降低温度对滞后现象有着相同的影响。
力学损耗:当应力的变化和应变一致时,没有滞后现象,每次形变所做的功等于恢复原状时取得的功,没有功的损耗。如果形变的变化落后于应力,发生滞后现象,则每一循环变化中就要消耗功,称为力学损耗,有时也称为内耗。
损耗功:拉伸和回缩时,外力对橡胶所做的功和橡胶对外所做的回缩功分别等于拉伸曲线和回缩曲线下的面积,一个拉伸-回缩循环中所损耗的能量与这两块面积之差相当。
橡胶的拉伸-压缩循环的应力应变曲线所构成的 闭合曲线常称为“滞后圈”,滞后圈的面积恰为单位体积的橡胶在每一个拉伸-压缩循环中所损耗的功。每一循环中,单位体积试样损耗的能量正比于最大应力、最大应变以及应力与应变之间相角差的正弦。因此,δ又称为力学损耗角,人们常用力学损耗角正切 tanδ表示内耗的大小。
影响内耗的因素:
结构:内耗的大小与高聚物本身的结构有关。顺丁橡胶内耗小,因为它的分子链上没有取代基团,链段运动的内摩擦阻力较小;丁苯橡胶和丁腈橡胶的内耗比较大,因为丁苯有庞大的侧苯基。丁腈橡胶有极性较强的侧氰 基,因而他们 的链段运动时内摩擦阻力较大。
温度:Tg以下,形变速度很快,内耗很小。温度升高,在向高弹态过渡时,高弹形变显著落后于应力的变化,内耗也大。温度进一步升高时,链段运动比较自由,内耗也小。在玻璃化转变区域将出现一个内耗的极大值,称为内耗峰,向粘流态过渡时,由于分子之间相互滑移,因而内耗急剧增加。
频率:频率很低时,高分子的链段运动完全跟得上外力的变化,内耗很小,高聚物表现出橡胶的高弹性;在频率很高时,链段运动完全跟不上外力的变化,内耗也很小,高聚物显得刚性,表现出玻璃态的力学性质;只有中间区域,链段运动跟不上外力的变化,内耗在一定的频率范围将出现一个极大值,这个区域中材料的粘弹性表现得很明显。
3.3典型粘弹性的实数模量和虚数模量与频率的关系:
可以看到在低频时,材料呈橡胶状,实数模量较小,且在一定频率范围内不随频率变化,在高频时,材料呈玻璃态,实数模量较高,也在一定频率范围内变化不大,在中间频率范围,材料呈现粘弹性,实数模量随频率急剧升高,虚数模量和tan σ则在粘弹区中都出现一个极大值,而在高频和低频时都很小。
3.4 粘弹性的力学模型
Maxwell模型:Maxwell模型由一个理想弹簧和一个理想粘壶串联而成。模型受力时,弹簧和粘壶受到的应力与总应力相等,而总应变等于两个元件的应变之和。
Maxwell模型的运动方程: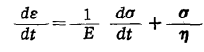
适用范围:线性聚合物的应力松弛过程。聚合物的动态力学行为(但是只要模量形状相符合,tanσ不符合)。
Maxwell模型不能模拟蠕变过程和交联高聚物的应力松弛过程。
Voigt模型:由一个理想弹簧和一个理想粘壶并联而成,应力是由弹簧和粘壶共同分担。总应力等于弹簧和粘壶受到的应力之和,弹簧和粘壶的应变相等,并等于总应变。
Voigt模型的运动方程: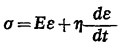
适用范围:交联聚合物的蠕变行为,模拟动态力学行为(但只有实数模量和虚数模量的形状是对的,tanσ形状不对)。
Voigt 模型不能用来模拟应力松弛过程,不适用于模拟线形高聚物的蠕变过程。
多元件模型:四元件模型线形高聚物的蠕变过程
3.5 时温等效原理
同一个力学松弛现象,既可在较高的温度、较短的时间内观察到,也可在较低的温度、较长的时间内观察到。因此,升高温度与延长观察时间对分子运动是等效的,对高聚物的粘弹行为也是等效的。可以借助于一个转换因子,将某一温度下测定的力学数据,转变成另一温度下的力学数据。
转换因子aT:移动因子与温度和参考温度有关,由WLF方程确定:
选择不同的温度作为参考温度,形式不变,但 C1、C2的值不同。若选择Tg作为参考温度,则C1和C2具有近似的普适值:C1=17.44,C2=51.6,
3.6 Boltzman 叠加原理
高聚物的力学松弛行为是其整个历史上所有松弛过程的线性加和。对于蠕变过程,每个负荷对高聚物形变的贡献是独立的,总的蠕变是各个负荷引起的蠕变的线性加和;对于应力松弛,每个应变对高聚物的应力松弛的贡献也是独立的,高聚物的总应力等于历史上诸应变引起的应力松弛过程的线性加和。根据这个原理,可以根据有限的实验数据,去预测高聚物在很宽的时间范围内的力学性质。
7.3.7 实验仪器和方法:
高温蠕变仪,应力松弛仪,动态扭摆仪,受迫共振法,受迫振动非共振法。
 加入华工考研各专业【微信交流群】 请加微信号:scutky8(备注年份+报考专业),获取免费直播课入场链接
加入华工考研各专业【微信交流群】 请加微信号:scutky8(备注年份+报考专业),获取免费直播课入场链接
|
|