|
|
好书推荐
832经济学
推荐指数:★★★★★
编者:
直系高分学长
推荐语:
高分研究生全程护航
每周考点
华工考研每周考点:主要是华工各专业考研核心考点,帮助大家快速把握考试关键,进行快速查缺补漏。
相关科目:832经济学
相关知识点:效用(1)
#1、效用(1)
主要内容
1.效用的相关概念:如何用效用来描述偏好、、如何判断函数的单调性
2.几种特殊形式的效用函数
3.边际效用:边际效用的微分表达、边际效用与边际替代率的关系
回忆偏好关系
1. x ≻y: 表示x严格偏好于 y。
2. x ~ y: 表示x 与 y受到同等偏好。
3. x ≿ y: 表示x至少和y受同等偏好。
完备性: 对于任意的两个消费束x和y,那么它们之间关系式x ≿ y 或者 y ≿ x
反身性:任何消费束至少与它本身受到同等偏好; 例如 x ≿ x
传递性:假如:x 弱偏好于y, 且y 弱偏好于z, 那么x 弱偏好于z; 例如:
x ≿ y 且y ≿ z→x ≿ z
1.效用函数
满足完备性、反身性、传递性和连续性的偏好关系可以通过一个连续效用函数来表示。
连续性表示消费束的微小变动只会引起偏好的微小变动。
2.效用的概念
在以消费者偏好为基础的消费者行为理论中,效用仅仅看作是描述偏好的一种数学方法。如何用效用来描述偏好?
3.1 效用函数
效用函数是为每个可能的消费束指派一个数字,它指派给受较多偏好的消费束的数字大于指派给受较少偏好的消费束的数字的方法。
对于消费束(x1,x2)的偏好超过对于消费束(y1,y2)的偏好,其充分必要条件是(x1,x2)的效用大于(y1,y2)的效用。
在现代经济学中,效用只不过是描述偏好的一种方式,即效用只不过是描述消费束的排列的一种方式。
效用函数就是按照一定的偏好特征给消费束赋值,使之保持一定的次序。在次序不变的情况下,可以有多种赋值方法。
3.2效用函数和无差异曲线
在偏好次序已知的情况下,能找到一种按偏好次序排列消费束的效用函数吗?
如果偏好不具有传递性;排除非传递偏好。通常能够找到效用函数表示性状良好的偏好
效用函数和无差异曲线的关系
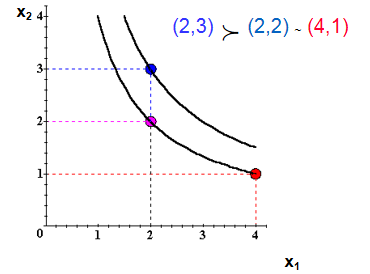
考虑以下消费束 (4,1), (2,3) and (2,2).
假设(2,3)≻(4,1) ~ (2,2).
分配给上述消费束保持偏好顺序的任何效用
e.g.U(2,3) = 6 > U(4,1) = U(2,2) = 4
这些被分配的效用称为效用水平。
无差异曲线表示相同偏好的消费束集合。
相同偏好Þ同样的效用水平
无差异曲线上所有消费束有同样的效用水平
因此消费束 (4,1) , (2,2) 是在同一条无差异曲线上,效用水平 U º 4。
消费束(2,3) 是在另一条无差异曲线上,效用水平 U º 6.
1.效用函数与无差异曲线
另一种表示这种偏好关系的方式为通过立体图在垂直方向显示效用值。
 通过加入两条无差异曲线可以使得三维图能更好地显示这种偏好关系。
3个消费束的消费与效用函数的三维图
比较更多的消费束会发现更多的无差异消费曲线,从而能使我们对消费者的偏好有更好的理解。
如前所述,可以通过在三维空间里面的垂直方向轴所表示的效用来描述每一条无差异曲线。
比较所有可能消费束可以得到消费者的所有无差异曲线,每一条曲线都有它的效用值。所有的这些无差异曲线完全代表了消费者的偏好。
关于给定偏好关系的所有无差异曲线的集合构成了无差异曲线图。一个无差异曲线图代表着一个效用函数,它们之间是相互对应的关系。
一个给定的偏好关系的效用函数不止一个。
假设 U(x1,x2) = x1x2 表示一种偏好关系。我们考虑消费束 (4,1),(2,3) 和 (2,2)。
U(x1,x2) = x1x2, 因此U(2,3) = 6 > U(4,1) = U(2,2) = 4; 也即, (2,3)≻(4,1) ~ (2,2).
U(x1,x2) = x1x2 → (2,3)≻(4,1) ~ (2,2).令 V = U2.
那么有 V(x1,x2) = x12x22 且 V(2,3) = 36 > V(4,1) = V(2,2) = 16同样,(2,3)≻(4,1) ~ (2,2).V 代表着与U相同的偏好顺序,因此表示相同的偏好。
U(x1,x2) = x1x2 → (2,3)≻ (4,1) ~ (2,2).
假设 W = 2U + 10.
那么 W(x1,x2) = 2x1x2+10 s因此W(2,3) = 22 > W(4,1) = W(2,2) = 18.
同样(2,3) ≻(4,1) ~ (2,2).
W 代表了和U和V一样的偏好顺序,因此也表示了相同的偏好关系。
——U 是一个表示≿偏好关系的效用函数
——f 是一个严格递增的函数,
那么 V = f(U)也同样是一个表示≿偏好关系的效用函数。
2.单调变换
单调变换就是在保持效用次序不变的条件下将一组数字变换成另一组数字的方法。
如果U代表偏好关系的效用函数;如果函数f是一个严格递增函数;V = f(U)代表的偏好与原函数U代表的偏好相同。
几种常见的正单调变换
如何判断函数是否是单调变换呢?
令u表示描述某种效用的方法,而f(u)是u的函数,如果df/du>0,即f(u2)- f(u1)与u2-u1始终同号,那么f(u)是u的单调变换。
例题
Jim的效用函数为:U(x,y)=xy,Jerry的效用函数为U(x,y)=1,000xy+2,000,Tammy的效用函数为U(x,y)=xy(1-xy),Oral的效用函数为U(x,y)=-1/(10+2xy)。Mark的效用函数为U(x,y)=x(y+1,000),Pat的效用函数为U(x, y)=0.5xy-10,000,Billy的效用函数为U(x, y)=x/y。Francis的效用函数为U(x,y)=-xy。问
a. 哪几位和Jim有相同的偏好?
b. 哪几位和Jim有相同的无差异曲线?
c. 请解释a和b答案的不同。

加入华工考研各专业【微信交流群】 请加微信号:scutky8(备注年份+报考专业),获取免费直播课入场链接
|
|