|
第二章 静定结构的受力分析 1.静定结构的一般性质:
(1)静定结构是无多余约束的几何不变体系,用静力平衡条件可以唯一的求得全部内力和反力。 (2)静定结构只在荷载作用下产生内力,其他因素作用时,只引起位移和变形。 (3)静定结构的内力与杆件的刚度无关。 (4)在荷载作用下,如果仅靠静定结构的某一局部就可以与荷载维持平衡,则只有这部分受力,其余部分不受力。 (5)当静定结构的一个内部几何不变部分上的荷载或构造做等效变换时,其余部分的内力不变。 (6)静定结构有弹性支座或弹性结点时,内力与刚性支座或刚性节点时一样。 解放思想:计算内力和位移时,任何因素都可以分别作用,分别求解,再线性叠加,以将复杂问题拆解为简单情况处理。
2.叠加院里的应用条件是: 用于静定结构内力计算时应满足小变形,用于位移计算和超静定结构的内力计算时材料还应服从胡克定律,即材料是线弹性的。
3.分段叠加法作弯矩图: (1)选定外力的不连续点为控制截面,求出控制截面的弯矩值。 (2)分段画弯矩图。 适用条件:既适用于静定结构,也适用于超静定结构,还适用于变截面的情况;但该法是以叠加原理为基础,因此只能适用于小变形和材料是线弹性的情况。
4.内力图的特点: (1)计算内力时,所截取的截面应垂直于杆轴,内力假设为正方向。 (2)内力图的坐标,应垂直于杆轴。 (3)直杆在无荷载的区段,M图为一斜直线,剪力图为一平行的直线。 微分关系: 铰节点上无荷载作用时,铰节点右侧的弯矩图,可以直接延伸过来获得另一侧的弯矩图。 (4)集中力偶M作用处,剪力无变化,M图有突变。 (5)当铰节点处作用力偶时,应看清力偶作用在铰的左侧还是右侧,力偶不能直接作用在铰上,只能作用在铰两侧的截面上。 (6)主从型结构,注意利用定向传力的性质。(作用在主结构上的力不引起附属结构的内力) (7)两端铰接的直杆,若跨内无横向荷载,则该杆只受轴力,无弯矩和剪力。
5.对称性的利用:(M、N正对称,FQ反对称) 非对称和反对称荷载,因为A点为铰接,力偶作用于A点左侧截面,该截面弯矩大小等于M,而A点右侧截面无力偶,故弯矩为零,即左右弯矩图不对称,所以该力偶是非对称荷载。
6.斜梁的计算:(于玲玲书P36) 简支斜梁当其荷载、杆长相同时,支座方向的改变对M、FQ图无影响,只对轴力图有影响。
7.绘制变形曲线的原则: (1)曲线的凸向应与弯矩图的受拉侧一致。 (2)刚结点连接的各杆变形后应保持夹角不变。 (3)不考虑轴向变形时,杆件变形后的投影长度应和原长相等。 (4)固定支座处变形曲线应与杆轴相切,而铰节点处应体现出转角。
8.使用结点法和截面法时,一定要注意观察截断的杆件是梁式杆还是链杆,两者的手里特点不同。尤其是取结点时易犯错,结点不能连接梁式杆,否则轴力与剪力均要考虑才能使之平衡。
9.拱的特点: (1)在竖向荷载作用下产生水平推力。 (2)因为水平推力的存在,使三铰拱的弯矩比相应简支梁的弯矩小。 (3)在竖向荷载作用下,梁的截面没有轴力,而拱的轴力较大,切一半为压力,因此,拱比梁更便于利用抗压性能好而抗拉性能差的材料。
10.拱的合理轴线: 在固定荷载作用下,使拱的各个截面弯矩都为零的轴线成为合理轴线。不同的荷载,对应着不同的合理轴线,对于三铰拱结构,任意荷载下都存在着与其相应的合理轴线。
11.桁架内力计算技巧。 (1)判断是否有零杆,以减少计算量。(充分利用对称性) (2)用截面法时,尽量利用截面单杆的概念,使一个方程只包含一个未知力。 (3)充分利用对称性简化计算。
12.求拱的合理轴线的公式:
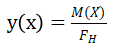
(1)三铰拱在沿水平线均匀分布的竖向荷载作用下,合理轴线为一抛物线。 (2)拱在均匀水压力作用下,合理轴线为圆弧,而轴力等于常数。 (3)在填土重量作用下,三铰拱的合理轴线是一悬链线。

加入华工考研各专业【微信交流群】 请加微信号:scutky8(备注年份+报考专业),获取免费直播课入场链接
|