|
分享研究生
J学长:
23级华工数学学院学硕专业上岸研究生,J学长,政治:70+ 英一:70+ 623数学分析:115+ 823高等代数:125+
课程模块 1.专业课参考书各章节考试重点及考察方式 2.知识点的学习和汇总,做题思路 3.解读往年真题题型结构和知识点
01 专业课参考书各章节考试重点及考察方式 一、数学分析: 【1】《数学分析》(上、下册),复旦大学数学系编,高等教育出版社;
【2】《数学分析》(上、下册),华东师范大学数学系编,高等教育出版社; 复旦陈纪修、谢惠民、
二、高等代数: 选读书目
【1】《高等代数》(第四版)北京大学数学系几何与代数教研室代数小组编,王萼芳、石生明修订,高等教育出版社 丘维声、复旦
点评华师大数分: 1.经典中文教材,是基础阶段最为适合使用的教材,适合基础比较薄弱的同学。 2.这本书定义定理框架结构较为清晰,例题详实,习题从简单到复杂排列:节后习题比章后习题简单,横线上的题目比横线下的习题简单,适合学完书上的知识点后及时巩固以及冲刺提高。 3.例题和课后习题都很经典,很多题会出现在考研真题中
点评北大高代: 1.经典中文教材,除了二次型章节写得都比较好。 2.课后习题含金量高,但有些过于基础,有些难度过大,只在每章后面统一编排了习题。 3.习题经典,考场上会出现原题。
1. 专业课参考书各章节考试重点及考察方式(频率统计) 章节一览,**号为重点,*号为一般章节,~为低频考察章节 1、实数集与函数 2、**数列极限 (23,1), (23,2), (21,2), (19,3) 3、*函数极限 (23,6), (19,1), (19,11), (19,13), (19,14) 4、*函数的连续性 (23,8) 5、导数和微分 (22,9), 6、**微分中值定理及其应用 (23,3), (22,10) 7、实数的完备性 (19,9), 8、~不定积分 9、~定积分 10、~定积分的应用 (22,2) 11、反常积分 (22,11)
12. 数项级数 (23,10) 13. 函数列与函数项级数 (23,11), (22,8), (19,10) 14. 幂级数 (22,1), (19,5), (19,12) 15. 傅里叶级数 (22,4)
16. 多元函数的极限和连续 (23,7), (19,7) 17. 多元函数的微分学 (23,5) 18. 隐函数定理及其应用 (22,6), (22,7), (19,2) 19. 含参量积分 (23,9), (19,8)
20.曲线积分 (22,3), (19,4), 21.重积分 (22,5) 22.曲面积分 (19,6), (23,4)
1.多项式 (23,1), (21,1), (20,1), (18,1) 2.行列式 (23,2), (21,2), (20,2), (18,2) 3.线性方程组 (23,3), (20,4), (18,3), (18,4), (18,6) 4.矩阵 (21,7), (21,8), (20,3), (18,8) 5.**二次型 (23,4), (23,8), (21,5), (20,5), (18,7) 6.线性空间 (23,5), (23,7), (21,6), (20,8), (18,5) 7.线性变换 (23,6), (21,3), (21,4), (20,6), (20,7) 8.~入-矩阵 9.欧几里得空间 10.双线性函数
19年、22年无公开整理出来的真题
1.多项式 最大公因式,互素 2.行列式 范德蒙行列式 3.线性方程组 有解判别定理、解的结构 4.矩阵 对称矩阵、 5.**二次型 与矩阵结合考察 6.线性空间 直和问题,维数公式 7.线性变换 特征值、不变空间 8.~入-矩阵 9.欧几里得空间 10.双线性函数




02 知识点的学习和汇总,分享快速记忆技巧 从定义出发,相关定理为其枝干
扩展并补充细节
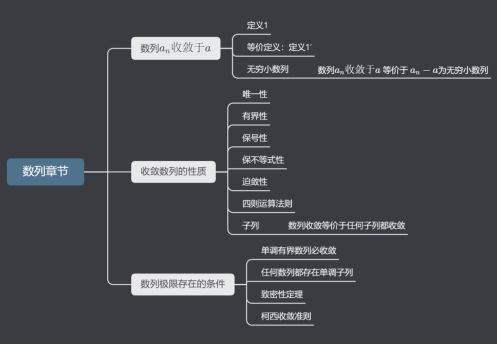
做思维导图 手写:印象相对深刻,不可修改 软件:不可修改
有名字的定理要重点关注!!
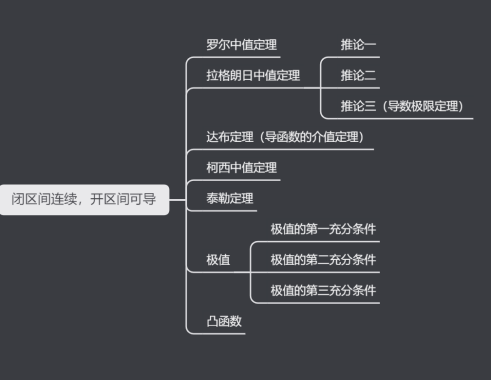
对于定理证明的学习,以一个经典的定理为例

在考场上如何找到做题思路 1.全面复习:书上的定义定理一个不落 定义是基本的概念性知识,定理往往是解题的关键
2.对各种题型和方法的积累,总结归纳
3.泛刷,查缺补漏 有些题目没有见过很难上手
好的学习习惯的养成: 1.多在空白草稿纸演算,写上当天日期 2.上午复习数分,下午复习高代 3.每复习一部分,要进行归纳总结
03 解读往年真题题型结构和知识点 1.题目数量(数学分析:11题;高等代数:8题)
2.考察内容(只能是较为全面的考察) 3.相关知识点
送分题出现的考察部分: 数学分析:数列极限(计算和证明)、极值问题、多元积分、多元函数极限与连续、极值问题
难题出现的考察部分: 数学分析:函数项级数、反常积分、含参量积分
高等代数:多项式、线性变换、线性空间




623数学分析历年出题风格较为稳定,但偶有”超纲题”、”怪题”,部分真题可在华师大数分、裴砖上找到原题。在这三本教材的基础上,再稍作重点练习即可。 题型分类: *极限:计算函数极限,数列极限 *多元函数:隐函数、链式法则、极值问题 *曲线积分、曲面积分、重积分 *级数:幂级数、函数项级数、数项级数、傅里叶级数 函数递推公式 微分中值 切线、法平面 含参量积分:计算、证明
823高等代数历年出题风格稳定,题目难度有下降的趋势,部分真题可在北大高代、樊启斌高等代数典型问题与方法上找到原题。在教材的基础上,在习题册上稍作练习即可。
题型分类: 多项式:整除、互素 行列式: 线性方程组 矩阵、二次型 线性空间 线性映射 欧式空间 双线性函数

|