|
题型分析 华工考研院联合华工学长学姐针对考研数学开设考点分析主题。本文着重讲解考研数学《线性代数》的重点,考研鹅可自行查缺补漏。
线性代数
第二章、矩阵 思考与点拨
矩阵及其运算是线性代数的核心,后续各章的基础,考点较多,重点考点是逆矩阵、伴随矩阵及矩阵方程,这几年还频频出现初等变换与初等阵的试题,应注意到的大致有以下几部分内容. 1.基本运算:要搞清概念,熟练掌握运算规则并保证运算的正确性,重点关注以下几点。 (1)搞清能否运算,怎样运算,运算结果是什么. (2)搞清数的运算、行列式的性质,与矩阵运算的区别. (3)充分利用运算规则,如计算中结合律、分配律的利用,但矩阵运算没有交换律,消去律.
2.逆矩阵:理解逆矩阵的概念,掌握运算法则,掌握矩阵可逆的充分必要条件,会证矩阵可逆,并能正确求出逆矩阵。 求逆矩阵的方法:对数值矩阵,一般有(1)公式法.A-1=1/︳A ︳A*,特别适用二阶矩阵;(2)初等变换法.[A ︳B]→[E ︳A].对抽象矩阵,一般有(3)定义法,化成AB=E,则A可逆,且A-1=B;(4)化成已知可逆矩阵的乘积,即若化成A=BC,其中B,C均是可逆阵,则A可逆,A-1=(BC)-1=C-1B-1. 证明A可逆的方法: A可逆⇔︳A ︳≠0⇔AX=0有唯一零解⇔AX=b有唯一解⇔r(A)=n⇔A的行(列)向量组线性无关,或用反证法。
3.伴随矩阵A*:理解伴随矩阵的概念,注意Ai j与A*的联系,能熟练得出A,A-1,A*,(A*)-1,︳A ︳,︳A*︳之间的关系,如 (1)︳A*︳=︳A ︳n-1,(2)若A可逆,(A*)-1=1/︳A ︳A,A*=︳A ︳A-1。 若公式中将A代入kA时,有 (kA)(kA)*=︳kA ︳E,得(kA)*=kn-1A*; 若公式中将A代入A*时,有 A*(A*)*=︳A*︳E,得(A*)*=︳A ︳n-2A. A*的秩只有n,1,0三种可能,且

4.矩阵方程:矩阵方程的试题较多,这类试题具有定的综合性,既考查了利用矩阵运算法则、性质等把方程化简,又考查了具体的数值计算。解这类试题要求分二步走,“先化简”,写出所求矩阵的最简表达式,再代入具体的数值矩阵,进行数值运算(如题2.3)。
5.初等变换、初等阵、矩阵的秩及等价矩阵理解初等变换的概念,了解初等阵及其性质,能将矩阵的初等变换表达成矩阵乘初等阵,反之能将矩阵乘初等阵翻译成作初等变换(如题2.1~2.3)理解矩阵秩的概念,掌握用初等变换求秩及逆矩阵的方法。
6.分块阵:了解分块阵及其运算,会求分块对角阵的n次幂及分块对角阵的逆等。
第三章、向量 思考与点拨
向量组的线性相关性是线性代数中的难点,也是考试的重点,考生应深刻理解线性相关性的内在的含义外,还应与线性表出、向的秩及线性方程组等相联系,从各个侧面加强对线性相关性的理解。 本章试题大致有以下四个部分:
1.向量的线性表出 向量β能否由向量组α1,α2,…αs,线性表出⇔方程组α1x1+α2x2+…αs x n=[α1,α2,…αs]X=An×s X=β是否有解,其解即是表出系数⇔r(A)和r(A︳β)是否相等。 若α1,α2,…αs线性无关,α1,α2,…αs,β线性相关,则β可由α1,α2,…αs线性表出,且表出法唯一。 若α1,α2,…αs线性相关,则至少存在一个向量αi可由其余向量线性表出。 向量组(I) β1,β2,…βs中任一个向量βi(1,2,…,s)都可由(Ⅱ) α1,α2,…αs线性表出,称向量组(I)可由向量组(Ⅱ)线性表出,两组向量可以相Ⅰ互表出,则称两向量组等价,等价向量组等秩,反之不成立。
2.向量组线性相关性的判别和证明 要说明或证明向量组α1,α2,…αs线性相关,只要求出(观察出)有不全为零的数k1,k2,…ks,使k1α1+k2α2+…+ksαs=0.即说明或证明方程组有k1α1+k2α2+…+ksαs=0有非零解。 证明一组向量α1,α2,…αs线性无关,有两类题型:(1)若题设条件中只有一组向量(附有一些其他条件),则应利用定义证明(实质上是反证法);(2)若已知一组向量线性无关,要证另一组向量也线性无关,则可以用定义证明,也可以用等价向量组、秩、方程组等方法证明(例题2.5)。
3.求向量组的极大线性无关组及向量组的秩 应理解向量组的极大线性无关组的概念,并掌握其求法。
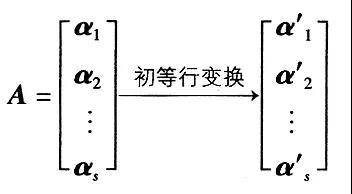
则向量组α1,α2,…αs和α1',α2',…αs'是等价向量组,等价向量组等秩。 A=[β1,β2,…βs][ β1',β2',…βs'], 则β1,β2,…βs与β1',β2',…βs'中任何对应的部分向量组有相同的线性相关性。向量组极大线性无关组不唯一,但极大无关组的向量个数是唯一的,此数即是向量组的秩。
4.向量空间,要求了解向量空间、子空间、解空间,基、维数,坐标等概念,了解基变换公式、坐标变换公式,会求过渡矩阵,掌握施密特标准正交化方法,这部分内容相对试题较少,从1987年考研数学统考以来,共出过4题,二个题是过渡矩阵的(例题1.1),一题是求解空间的标准正交基,一题是求一个向量在一组基下的坐标。
加入华工考研各专业【微信交流群】 请加微信号:scutky8(备注年份+报考专业),获取免费直播课入场链接
|